Soal 1 tugas UAS Optimasi
Referensi : Optimasi Tak Linear , Oleh Dr. H.A. Parhusip, Penerbit: Tisara
Grafika Salatiga (2014)
PENYELESAIAN PERMASALAHAN OPTIMASI
NONLINEAR BERKENDALA DENGAN METODE PENGALI LAGRANGE
1. Tujuan [kembali]
Secara umum masalah optimasi yag berkendala berbentuk:
Dengan kendala:
Untuk menyelesaikannya maka dibentuk
fungsi lagrange
Kemudian pecahkan sistem n + m dengan persamaan
dan
Teorema 1.11: untuk masalah (1.10)
dapat diselesaikan asalkan f(x) dan gi(x) (i = 1,2,...,m) memiliki
turunan parsial pertama yan kontinu dan mariks Jacobi m x n dengan memiliki
rank m di
Metode pengali Lagrange ini ekuivalen
dengan menggunakan persamaan kendala untuk menghilangkan beberapa variabel x
tertentu dari fungsi obyektif dan kemudian memecahkan persoalan maksimisasi
tanpa kendala dalam variabel-variabel x yang tersisa.
Minimalkan dengan metode pengali Langrange untuk masalah fungsi tujuan dengan kendala persamaan,
Mengganti kendala persamaan x2 = 2 - x1,
sehingga menjadi optimasi tal terkendala sebagai
maka dapat dengan mudah dipecahkan dengan
menetapkan turunan dari hal ini.
atau
Gambar 1. Fungsi
Obyektif dengan kendala contoh permaslahan
Program MATLAB untuk mengilustrasikan gambar 1 sebagai berikut:
clear
close all
[X,Y] = meshgrid(-3:.125:3);
Z = X.^2 + Y.^2;
meshc(X,Y,Z);
hold on
Z2=X + Y-2;
meshc(X,Y,Z2);
hold off






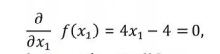


Tidak ada komentar:
Posting Komentar