Dimisalkan x adalah
variabel penentu dan f(x) adalah fungsi tujuan dari suatu masalah. Metode
optimasi menyelesaikan masalah:
Untuk menyelesaikan
permasalahan seperti tertera di atas digunakan kalkulus diferensial yang
dinyatakan seperti di bawah ini:
Misalkan f adalah
fungsi yang menerus dalam interval tertutup [a,b] dan dapat diderivasikan pada
interval terbuka (a,b).
(i) Jika f’(x) > 0
untuk seluruh x dalam (a,b), maka f adalah menanjak pada [a,b].
(ii) Jika f’(x) < 0
untuk seluruh x dalam (a,b), maka f adalah menurun pada [a,b].
Test derivasi pertama:
Misalkan f adalah fungsi yang menerus dalam interval tertutup [a,b] dan dapat
diderivasikan pada interval terbuka (a,b) kecuali mungkin di titik c yang
berada didalam (a,b).
(i) Jika f’(x) > 0
untuk a < x < c dan f’(x) < 0 untuk c < x < b, maka f(c) adalah
sebuah maximum lokal dari f.
(ii) Jika f’(x) < 0
untuk a < x < c dan f’(x) > 0 untuk c < x < b, maka f(c) adalah
sebuah minimum lokal dari f.
(iii) Jika f’(x) < 0
atau f’(x) > 0 untuk setiap x dalam (a,b) kecuali x = c, maka f(c) BUKAN
sebuah nilai ekstrim.
Test derivasi kedua:
Misalkan f adalah fungsi yang dapat diderivasikan pada interval terbuka yang
berisi titik c dan f’(c) = 0,
(i) Jika f”(c) < 0,
maka f(c) adalah sebuah maximum lokal dari f.
(ii) Jika f”(c) > 0,
maka f(c) adalah sebuah minimum lokal dari f.
Contoh 1:
Sebuah perusahaan
catering (makanan ringan yang menyediakan konsumsi untuk suatu penataran di JTE
FT UMY) berusaha mengurangi pengeluaran untuk keperluan pembungkus. Bungkus
tersebut terbuat dari kertas karton seperti tampak pada Gambar di samping.
Keempat pojoknya akan dipotong segi empat samasisi sedemikian rupa sehingga
volumenya menjadi maksimum.

Dari contoh di atas
tampak bahwa dengan cara analitis kalkulus diferensial nilai x yang memberikan
nilai f maximum dapat dicari tanpa mengetahui nilai dari f itu sendiri.
Untuk melengkapi
teorema optimasi nonlinier satu variabel yang telah dijelaskan di atas
disajikan teorema yang dapat digunakan untuk menentukan titik-titik ekstrem
dari suatu fungsi satu variabel.
Teorema:
Misalkan f’(c) = f”(c)
= … = f(n-1)(c) = 0, tetapi f(n)(c) ≠ 0. Maka f(c) adalah:
(i) nilai minimum dari
f(x), jika f(n)(c) > 0 dan n adalah bilangan genap,
(ii) nilai maximum dari
f(x), jika f(n) (c) < 0 dan n adalah bilangan genap,
(iii) bukan minimum dan
maximum jika n adalah bilangan gasal.
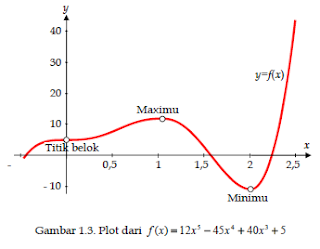
Contoh 2.
Tentukan maximum dan
minimum dari fungsi di bawah ini
Penyelesaian:
Cara analitis yang
diterapkan pada permasalahan optimasi satu variabel dapat pula diterapkan
kepada permasalahan multi variabel.
Secara umum teknik yang
digunakan pada optimasi satu dimensi dapat digunakan dalam optimasi multi
variabel.
Definisi dan
simbol-simbol yang digunakan:
Teorema:
Jika f(X) mempunyai
sebuah titik ekstrem (minimum maupun maximum) pada X = X* dan jika derivasi
pertama dari f(X) mempunyai nilai pada titik X*, maka ∇f(X*) = 0
PERHATIAN: Kebalikannya
belum tentu benar yaitu jika ∇f(X*) = 0 maka X*
adalah titik ekstrem.
Teorema:
Titik X* disebut titik
maksimum lokal dari f(X) jika dan hanya jika:
(i) ∇f(X*) = 0
(ii) H(X*) < 0
definit negatif dengan H = matrik Hessian yang didefinisikan sebagai:
Teorema:
Titik X* disebut titik
minimum lokal dari f(X) jika dan hanya jika:
(i) ∇f(X*) = 0
(ii) H(X*) > 0
definit positif atau |H|j > 0 untuk j = 1,2,…,n, sehingga
Contoh 3:
Tentukan titik-titik
ekstrim dari fungsi:
Pada bagian ini akan
didiskusikan teknik optimasi multi variabel dengan kendala persamaan yang
mempunyai bentuk umum sebagai berikut:
disini m ≤ n, jika
terjadi bahwa m > n, maka biasanya tidak dapat diselesaikan
Untuk menyelesaikan
permasalahan optimasi di atas, digunakan metode pengali Lagrange, yaitu:
Teorema:
Syarat perlu bagi
sebuah fungsi f(X) dengan kendala gj(X) = 0, dengan j = 1, 2, …, m
agar mempunyai minimum relatif pada titik X* adalah derivasi parsial pertama
dari fungsi Lagrangenya yang didefinisikan sebagai L = L(x1,x2,…,xn,
λ1,λ2,…,λn) terhadap setiap argumennya
mempunyai nilai nol.
Teorema:
Syarat harus bagi
sebuah fungsi f(X) agar mempunyai minimum (atau maximum) relatif pada titik X*
adalah jika fungsi kuadrat, Q, yang didefinisikan sebagai
dievaluasi pada X = X*
harus definit positif (atau negatif) untuk setiap nilai dX yang memenuhi semua
kendala.
Syarat perlu agar
menjadi definit positif
(atau negatif) untuk setiap variasi nilai dX adalah setiap akar dari
polinomial, zi, yang didapat dari determinan persamaan di bawah ini harus
positif (atau negatif).
Contoh 4:
Sebuah perusahaan
pelumas ingin membuat kaleng pelumas dari seng. Kaleng berbentuk silinder
dengan bahan yang terpakai seluas A0 = 24π. Berapa maximum volume kaleng yang
dapat dibuat dari bahan yang tersedia?
Penyelesaian
Pada bab ini akan didiskusikan teknik optimasi multi variabel dengan kendala pertidak-samaan yang mempunyai bentuk umum sebagai berikut:
Kunci dari penanganan
permasalahan di atas adalah merubah kendala pertidak-samaan menjadi persamaan
dengan menambah variabel slack. Jadi permasalahan optimasi di atas dapat ditulis
kembali sebagai:
Permasalahan ini dapat
diselesaikan metode pengali Lagrange. Untuk itu, dibentuk fungsi Lagrange
sebagai berikut:
Syarat perlu untuk
suatu penyelesaian optimum pers diperoleh dari penyelesaian sistem persamaan di
bawah ini.
Syarat perlu agar
persamaan optimasi, mencapai titik minimumnya dapat pula dicari dengan syarat Kuhn-Tucker.
Syarat ini perlu tetapi secara umum bukan merupakan syarat cukup untuk mencapai
minimum. Tetapi untuk problema jenis konvex, syarat Kuhn-Tucker menjadi syarat
perlu dan cukup untuk sebuah minimum global.
PERHATIAN:
Jika permasalahannya
adalah memaksimumkan {bukan meminimumkan seperti contoh}, maka λj ≤ 0 dalam
Pers.(1.21d).
Jika kendalanya adalah
gj ≥ 0, maka λj ≤ 0 dalam Pers.(1.21d).
Jika permasalahannya
adalah memaksimumkan dan jika kendalanya adalah gj ≥ 0, maka λj ≥ 0 dalam
Pers.(1.21d).
Contoh 5:
Sebuah perusahaan
pembuat komputer mendapat kontrak untuk menyediakan 50 unit komputer pada akhir
bulan pertama, 50 unit komputer pada akhir bulan kedua, dan 50 unit komputer
pada akhir bulan ketiga. Biaya produksi x buah komputer tiap bulannya adalah
x2. Perusahaan ini dapat memproduksi komputer lebih dari yang dipesan dan
menyimpannya di gudang untuk diserahkan pada bulan berikutnya. Biaya gudang
adalah sebesar 20 satuan harga untuk tiap komputer yang disimpan dari bulan
yang lalu kebulan berikutnya. Diandaikan bahwa pada permulaan pesanan di gudang
tidak terdapat persediaan komputer. Tentukan jumlah produksi komputer tiap
bulannya agar biaya pembuatannya minimum.




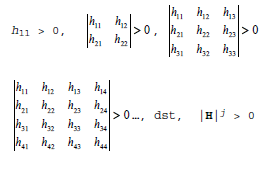




















Tidak ada komentar:
Posting Komentar